
Los números reales pueden clasificarse en dos tipos de diferentes maneras, por ejemplo, como hemos visto en la entrada anterior en racionales e irracionales, o en algebraicos y transcendentes.
Llamamos números construibles a los números que con ayuda de los instrumentos clásicos de dibujo (regla y compás) y, sólo éstas, se pueden representar sobre una recta en la que hemos señalado dos puntos que representan al 0 (origen) y al 1 (unidad de medida). Todos los números racionales son construibles y algunos irracionales también.
Un número decimos que es algebraico, si es raíz de una ecuación polinómica, por ejemplo el número 5 es algebraico, pues puede obtenerse como solución de la sencilla ecuación: 2x – 10= 0; También lo es “el número áureo” , que además es irracional, pues se obtiene como solución de la ecuación cuadrática:
Nota: Sobre este número y sus construcciones, así como las que origina puede verse en este blog el post: La divina proporción.
Todos los racionales son algebraicos, y, también lo son todos los irracionales construibles. Al revés no es cierto, de manera que los números construibles son un subconjunto estricto o propio (no igual) de los algebraicos. Los números transcendentes son el resto, entre los que se encuentran los famosos pi, e,…
Cantor probó que la clase de los números algebraicos, que es mucho más extensa que la de los números racionales, tiene sin embargo, la misma potencia que el conjunto de los números naturales: ℵ0, es decir, es un conjunto infinito numerable. Por lo tanto, son los números transcendentes los que les dan al sistema de los números reales el fuerte carácter de densidad que trae como consecuencia su potencia más alta.
En resumen, podemos decir:
• Dentro del conjunto de los irracionales existe un conjunto de números que no son algebraicos. A esos números los llamamos trascendentes.
• Como los números algebraicos son numerables, el resto de números reales, los trascendentes, tienen que tener la potencia del continuo.
Una vez que en 1874, Cantor demuestra que el cardinal del conjunto de los naturales es estrictamente menor al de los números reales y, después de analizar la numerabilidad de los conjuntos de números algebraicos y transcendentes. Lo siguiente a preguntarse es si existen conjuntos cuyo cardinal esté incluido estrictamente entre el de ambos conjuntos, es decir:
¿Existe algún conjunto A, cuyo tamaño sea MAYOR que el de los números naturales, pero MENOR que el de los números reales?

Cantor nos responde con “La hipótesis del continuo” (en lo sucesivo HC).
HC: “No existen conjuntos cuyo tamaño esté comprendido estrictamente entre el de los Naturales y el de los números Reales”.

Cantor trató en vano demostrar la hipótesis del continuo, era sólo una “conjetura”.

La demostración (o negación) de la Hipótesis del Continuo es uno de los 23 problemas de Hilbert (de hecho, es el primero), algunos de los cuales todavía no han sido resueltos. Fueron propuestos por Hilbert en 1900 como desafío a las generaciones presentes y futuras de matemáticos.
Al igual que la geometría euclídea se sustenta en un “paquete” de postulados o axiomas, la Teoría de Conjuntos también lo hace en base a un sistema de axiomas que denominamos Axiomática Zermelo-Fraenkel, en lo sucesivo axiomática ZF; Cuando añadimos a este conjunto de axiomas el llamado y muy cuestionado “Axioma de elección”, el sistema lo notamos por ZFC.

Pues bien, el no menos genial Kurt Gödel demostró en 1940 que no se podía demostrar como falsa la hipótesis del continuo partiendo de la axiomática ZF (Zermelo-Fraenkel), incluso si se añadía el Axioma de Elección (ZFC). Pero, años más tarde, en 1963, Paul Cohen, demostró, a su vez, lo contrario, esto es: que tampoco podía probarse su veracidad partiendo de dichos axiomas. Así pues, la HC es indecidible (indemostrable): ni puede afirmarse, ni puede negarse.

Dicho de otro modo Gödel nos asegura que puede construirse una teoría de conjuntos consistente donde la HC fuese cierta y, simultáneamente Cohen también nos asegura la construcción de una teoría de conjuntos consistente donde la HC es falsa. Es decir, obtenemos sistemas axiomáticos consistentes en ambos casos. Una situación análoga a la que se obtiene cuando en geometría admitimos como cierto el quinto axioma o postulado de las paralelas o lo negamos en todas sus formas posibles, el resultado provoca la existencia de geometrías distintas y consistentes, las llamadas geometrías no euclídeas: la propia euclídea, la debida a Riemann (Geometría elíptica) y la de Bolyai-Lobachevsky (Geometría hiperbólica).

Hemos visto en este trayecto como la densidad determina la cardinalidad o potencia de un conjunto. Cantor, nos sube ahora un peldaño de su particular escalera y comienza a plantearse si la dimensión determina de alguna manera la potencia de un conjunto.
Nota:
En matemáticas decimos que una recta es un objeto de dimensión 1 (un punto de una recta viene determinado por un número real), un plano de dimensión 2 (un punto del plano viene determinado por dos números reales), el espacio tridimensional de dimensión 3 (un punto de nuestro espacio cotidiano viene determinado por una terna de números reales: tres), etc.
Y nos propone la pregunta: ¿Dónde hay más puntos en un segmento o en un cuadrado?
O, aún más fuerte: ¿dónde hay más puntos, en un segmento, en un cuadrado o en un cubo?

De nuevo nos pone la imaginación a prueba.
Y, Cantor de nuevo destroza la intuición con su imponente genio, demostrando que:
“El segmento, el cuadrado y el cubo (objetos de dimensiones distintas) poseen la misma potencia: la potencia del continuo, ℵ1”.
Para ello, en un derroche de elegancia propone el siguiente emparejamiento (biyección de nuevo) entre los puntos del segmento [0,1] y los del cuadrado que tiene por lado la misma longitud que el segmento, esto es: 1.

Si tomamos un punto cualquiera de la superficie del cuadrado de coordenadas (x,y), ocurrirá, por como ha sido construido el cuadrado que, x e y serán números reales entre el 0 y el 1.
Tomemos en particular un punto concreto del cuadrado, el de la imagen:
(x,y)=(0,3143256408876…, 0,6244356998124…)
Cantor asocia ahora este punto con un único punto del segmento [0,1] del siguiente modo:
El nuevo número “r”, se obtiene alternando los decimales de x e y, así, su primera cifra decimal será la primera cifra decimal de x, su segunda cifra decimal será la primera cifra decimal de y, la tercera cifra decimal será la segunda de x, la cuarta la segunda de y, la quinta la tercera de x,…y de nuevo “así sucesivamente”.
El número que hemos construido “r”, será:
r=0,36124434235566490988817264…
De este modo ni un solo punto del cuadrado se quedará sin pareja en el segmento. La biyección está establecida y, por tanto, la potencia del cuadrado coincide con la del segmento [0,1], que como ya hemos visto es ℵ1.
Y, ¿qué ocurre con el cubo?, pues exactamente igual:

En este caso, tenemos un punto (x,y,z) del espacio tridimensional de coordenadas:
x=0,3143256408876…, y=0,6244356998124…, Z=0,7763423906215…
El nuevo número “r”, se obtiene de nuevo alternando los decimales ahora de x, y, z así, su primera cifra decimal será la primera cifra decimal de x, su segunda cifra decimal será la primera cifra decimal de y, la tercera cifra decimal será la primera de z, la cuarta la segunda de x, la quinta la segunda de y, la sexta la segunda de z,…y de nuevo “así sucesivamente”.
El número que hemos construido “r”, será:
r=0,367127446343234552663499090…
Y de este modo establecemos otra biyección que permite asegurar que la potencia del cubo coincide con la del segmento [0,1], es decir, ℵ1.
¡Sorprendentemente, aunque se amplíe el conjunto de puntos de un segmento al de los puntos de un cuadrado o un cubo, no hay más puntos en el cubo ni en el cuadrado que en el segmento, por más raro que esto resulte no incrementamos realmente el número de objetos con los que trabajamos!
Este resultado que puede ampliarse al hiper-espacio (Espacio de dimensión 4) o a otros de mayor dimensión, chocaba tan frontalmente con la intuición que Cantor mismo escribía en una ocasión a Dedekind, en 1877 con ocasión, precisamente de su construcción de la biyección entre el segmento y el cuadrado: <<Je le vois, mais je ne le crois pas>> (<<Lo veo pero no lo creo>>), y le pedía vehementemente a su amigo que revisase cuidadosamente la demostración.
Pero el incansable Cantor, sigue subiendo peldaños y ahora, a la vista de los resultados, piensa si las dos únicas potencias son la de los naturales ℵ0 y la del continuo ℵ1, y se pregunta:
¿Existirán conjuntos con un cardinal o potencia mayor que ℵ1?

La respuesta es afirmativa y en la próxima y espero que última entrada sobre este apasionante tema, veremos de qué conjuntos se trata.
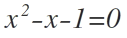
EL PARAÍSO DE CANTOR.
Es un deleite, el discurso con el lenguaje de Cantor.
Humildemente, diré, que, la solución de la inecuación, con la relación «mayor o igual» que infinito, es posible.
pjbf/////////
Me gustaMe gusta
Wooooooo no puede ser, por favor tome un poco de su valioso tiempo y escriba la parte faltante. Gracias
Me gustaMe gusta
Coincido con Ernesto Jimeno Frattini. Gran divulgador. Espero ansioso la quinta entrega de los números transfinitos.
Me gustaMe gusta
Quise decir con la «Parte V», supuestamente la última de la serie
Me gustaMe gusta
Falta de tiempo, está pendiente. Gracias por tu amable comentario. Un afectuoso saludo.
Me gustaMe gusta
Eres muy bueno, tío, con una gran capacidad didáctica ¿qué ha pasado con la Parte IV?
Me gustaMe gusta